Las potencias son bastante útiles, pues nos permiten abreviar la cantidad de veces en la que se multiplica un número por sí mismo. Si deseas conocer cuáles son las leyes de los exponentes para aplicarlas en la resolución de problemas, a continuación podrás aprenderlas y ver algunos ejemplos.
¿Qué son las leyes de los exponentes?
Las leyes de los exponentes también son conocidas como reglas de los exponentes. Estas leyes o reglas explican cómo se deben resolver los diferentes casos en los que tengamos una potencia o exponente, también llamado índice.
La potencia, exponente o índice es un pequeño número que aparecerá al lado derecho superior de un número, conocido como base. Este pequeño número indica la cantidad de veces que la base debe ser multiplicada por sí misma.
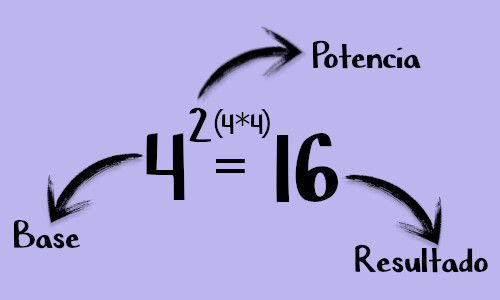
Como se puede apreciar en la imagen anterior, la base es 4 y el exponente o potencia es 2, por lo tanto, la base (4) debe multiplicarse dos veces por sí misma. Siendo así, el resultado es 16 (4*4 = 16).
No obstante, en el caso de que el exponente sea negativo, en lugar de una multiplicación se tendrá que dividir, y si el exponente es una fracción, se debe transformar en una raíz n-ésima.
¿Cuáles son las leyes de los exponentes? (Ejemplos)
Las leyes de los exponentes explican lo anteriormente señalado. A continuación encontrarás las distintas leyes o reglas de los exponentes que te ayudarán a comprender cada caso para así resolver los distintos problemas que se planteen.
Primera ley: Potencia de exponente igual a 1
La primera ley es la que dice que X 1= X, es decir, si el exponente es 1 el resultado de la potencia será igual al de la base. Ejemplo:
3 1 = 3
108 1 = 108
356 1 = 356
Segunda ley: Potencia de exponente igual a 0
Cuando el exponente es 0 y la base distinta de 0, el resultado será 1 (X 0 = 1). Ejemplo:
1 0 = 1
58 0 = 1
234 0 = 1
Sin embargo, si la base es igual a 0 y el exponente es 0, el resultado es indeterminado (0 0 = indeterminado)
Tercera ley: Exponente negativo
En el caso de que el exponente sea negativo (X -n) el resultado será una fracción (X -n = 1/X n) en donde el numerador será 1 y el denominador será la potencia. Ejemplo:
5 -3 = 1/5 3 = 1/125
8 -2 = 1/8 2 = 1/16
3 -6 = 1/3 6 = 1/729
Cuarta ley: Multiplicación de potencias de igual base
Cuando tenemos dos potencias de igual base diferentes de 0 y se deben multiplicar, solo se suman los exponentes y la base se mantiene igual (X m *X n = X m’+n). Ejemplo:
3 3 * 3 2 = 3 3+2 = 3 5
8 12 * 8 2 = 8 12+2 = 8 14
10 4 * 10 6 = 10 4+6 = 10 10
Quinta ley: División de potencias de igual base
En caso de la división de potencias de igual base diferentes de 0, se restan los exponentes y la base se mantiene igual (X m / X n = X m-n). Ejemplo:
2 5 / 2 2 = 2 (5 – 2) = 2 3
7 8 / 7 7 = 7 (8 – 7) = 7 1
13 4 / 13 2 = 13 (4 – 2) = 13 2

Sexta ley: Multiplicación de potencias con base diferente
Cuando se multiplican potencias con base diferente e igual exponente, se mantiene el exponente y se multiplican las bases [X m * Y m = (X*Y) m]; o en caso de que una multiplicación esté elevada a una potencia, cada uno de los términos pasaría a estar elevado a determinado exponente [(X*Y) m = X m * Y m). Ejemplo:
6 8 * 8 8 = (6*8) 8 = 48 8
12 5 * 23 5 = (12*23) 5 = 276 5
(5*3) 4 = 5 4 * 3 4 = 15 4
Séptima ley: División de potencias con diferente base
Al igual que sucede en el caso anterior pero con división, si la división de potencias es con bases diferentes, el exponente se mantiene y se dividen las bases [X m / Y m = (X / Y) m]; y si la división está elevada a una potencia, ambos términos se elevan a esa potencia y se dividen [(X/Y) m = X m / Y m]. En caso de que el exponente sea negativo, se invierte el numerador con el denominador [(X/Y) –m = (Y/X) m = Y m / X m]. Ejemplo:
16 5 / 4 5 = (16/4) 5 = 4 5
(4/2) 3 = 4 2 / 2 2 = 2 2
(4/5) -8 = (5/4) 8 = 5 8 / 4 8
Octava ley: Potencia de una potencia
Cuando una potencia está elevada a una potencia, los exponentes se multiplican y la base se mantiene [(X m) n = X (m*n)]. Ejemplo:
(2 3) 5 = 2 (3*5) = 2 15
(30 8) 4 = 30 (8*4) = 30 32
(5 2) 7 = 5 (2*7) = 5 14
Novena ley: Exponente fraccionario
En caso de que la potencia tenga un exponente fraccionario, se debe transformar a una raíz n-ésima en donde el numerador de la potencia se mantiene como exponente y el denominador pasa a ser el índice de la raíz ![]() Ejemplo:
Ejemplo:
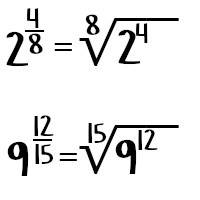

Si quieres aprender a aplicar las leyes de los exponentes, será necesario que realices varios ejercicios. En este archivo PDF podrás encontrar unos cuantos ejercicios resueltos para que puedas practicar. Quizá también te interese aprender las leyes de los radicales, ya que para la novena ley de los exponentes serán necesarias.
