Al igual que la ley de senos y ley de cosenos, la ley de tangente es útil para resolver triángulos oblicuos. Si quieres aprender a utilizar la ley de tangente, a continuación podrás conocer en qué consiste esta ley, cuáles son sus fórmulas y mucho más. Al final encontrarás un ejemplo y un archivo PDF con ejercicios que te ayudarán a practicar.
¿Qué es la ley de tangente?
La ley de tangente o teorema de la tangente es un teorema de la trigonometría que permite conocer los lados y ángulos de un triángulo oblicuo. Por lo tanto, puede ser utilizado al igual que la ley de senos y la ley de cosenos. Cabe señalar que si bien este teorema es menos conocidos, es igualmente útil.
Para aplicar la ley de tangente se deben conocer dos lados del triángulo y un ángulo, por ejemplo, conocer a, b y C; o bien, dos ángulos y uno de los lados del triángulo, como por ejemplo tener los valores de A, B y c. De otro modo, tendríamos que aplicar los otros dos teoremas de la trigonometría. Recuerda que las minúsculas son para los lados del triángulo y las mayúsculas corresponden a los ángulos.
Fórmulas de la ley de tangente
La ley de tangentes nos dice que el cociente entre la suma y resta de dos lados de un triángulo es igual a la razón entre la tangente de la semidiferencia de los ángulos opuestos a cada uno de los lados y la tangente de la mitad de la diferencia de estos ángulos. Siendo así, las fórmulas del teorema de tangentes son:

Ejemplos de la ley de tangente
Con solo conocer la teoría del teorema de la tangente es un poco complicado comprender en qué consiste esta ley. No obstante, mediante algunos ejemplos y ejercicios será mucho más sencillo. Te explicaremos el siguiente ejercicio para que puedas entender mejor cómo aplicar la ley de la tangente.
En el siguiente ejemplo tenemos un triángulo en el que solo conocemos el ángulo A, el ángulo C y el lado c. Por lo tanto, tenemos que calcular el ángulo B y los lados a y b para resolver el triángulo.
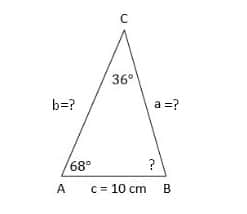
Para ello, aplicaremos el teorema de tangente usando la fórmula que vimos anteriormente. Seguidamente sustituiremos los valores y seguiremos con el procedimiento que se explica a continuación para poder hallar el valor de a.

Ahora que hemos calculado el valor del lado a podemos proceder a calcular el ángulo B que es el único que nos falta, pues ya tenemos A y C. Por lo tanto, solo tenemos que realizar el siguiente procedimiento. Teniendo en cuenta que la suma de todos los ángulos de un triángulo da 180º, esto es más sencillo.

Una vez que tenemos el lado a y el ángulo B, ya solo nos falta calcular el lado b. Para ello volvemos a aplicar el teorema de la tangente. Por ende, utilizamos una de las fórmulas vistas previamente y continuamos con el procedimiento, tal como se muestra a continuación.

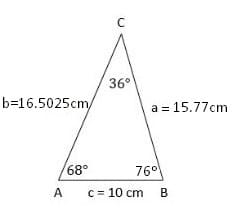
Finalmente, y como podrás comprobar, ya hemos calculado todos los datos que faltaban de nuestro triángulo oblicuángulo. Es así que hemos resuelto el problema y aplicado correctamente el teorema de tangente.
Aplicaciones de la ley de tangente
Al igual que con la ley de cosenos y la ley de senos, el teorema de tangentes puede aplicarse en diversos ámbitos de la vida real. Como se trata de un teorema de la trigonometría, es de gran utilidad para resolver triángulos oblicuos u oblicuángulos. Por lo tanto, puede utilizarse para determinar la distancia que hay entre un edificio a otro, calcular la altura de un árbol, y mucho más.
Si bien esta función trigonométrica es igualmente útil, no es tan extendida como el seno y el coseno, los cuales suelen explicarse más en clases de matemáticas que el propio teorema de la tangente. En algunos casos es posible que en lugar de usar la ley de tangente puedas optar por usar las otras dos funciones trigonométricas.
Si deseas aprender más y hallar distintos ejercicios para practicar, en este archivo PDF encontrarás ejercicios del teorema de la tangente, del seno y del coseno. Recuerda que la práctica te permitirá resolver con mayor rapidez los ejercicios, pues comprenderás mejor cómo aplicar este teorema.
