El Teorema de Bayes fue inventado por el teólogo Thomas Bayes en el siglo XVIII para dar resolución a problemas triviales, en este teorema se aplica la probabilidad condicionada, refiriéndose a la probabilidad de ocurrencia de una hipótesis, dependiendo de la presencia de nueva evidencia.
Desde hace muchos años hasta la actualidad, ha sido utilizado para representar matemáticamente la relación entre lo que se conoce y lo que se puede revelar ante nosotros, con la finalidad de poder mejorar la forma en la que tomamos algunas decisiones.

Debido a la efectividad del Teorema de Bayes para reducir la expectativa acerca de un hecho, este se ha utilizado en muchos lugares del mundo para establecer la probabilidad de que se tenga una condición médica exigiendo el resultado positivo de un examen, para determinar el posible ganador de elecciones e incluso ha sido usado para conocer la inexistencia o existencia de Dios.
Explicación de la fórmula del Teorema de Bayes
El Teorema de Bayes se utiliza en pocas palabras como una prueba de fuerza, entre dos hipótesis que compiten una con otra y a partir de estas poder determinar la probabilidad de ocurrencia, conociendo nueva evidencia, la fórmula de este teorema es sencilla y más fácil de comprender de lo que parece.

Te explicaremos el significado de cada una de las partes o variables de la fórmula del Teorema de Bayes:
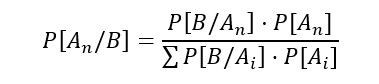
En esta fórmula B es el hecho sobre el que se tiene una información prevía y A(n) son los sucesos condicionados, es decir, los que pueden ocurrir dependiendo de B.
En el numerador de la fórmula se encuentra toda la probabilidad condicionada y en el denominador, la probabilidad total, a pesar de parecer complicada es realmente muy sencilla.
Ejemplo para explicar el Teorema de Bayes
En este ejemplo no se utilizará la variable A(n) de esa manera, sino que sera sustituida por A,B y C:
Una empresa tiene la filial de su fábrica en España y este dispone de tres maquinas A, B y C en las que se producen envases utilizados para el embotellamiento de agua.
Ya se conoce que la máquina A sólo produce un 40% de la cantidad total de botellas, la maquina B produce un 30% y en la máquina C 20%, además de esto se sabe que cada una de las máquinas produce envases con defectos.
Tomando en cuenta entonces que la máquina A produce un 2% de envases con defectos sobre el total, la máquina B un 3% y la máquina C un 5%, se plantea los siguiente:
P(A)=0,40 Produccion de la máquina A
P(B)= 0,30 Producción de la máquina B
P(C)= 0,20 Producción de la máquina C
P(D/A)= 0,02 Produccion de envases defectuosos de la máquina A
P(D/B)= 0,03 Produccion de envases defectuosos de la máquina B
P(D/C)= 0,05 Producción de envases defectuosos de la máquina B
Si un envase ha sido fabricado en la empresa en España ¿Cuál es la probabilidad de que sea defectuoso?
Se debe calcular primero la probabilidad total y luego con todo el Teorema de Bayes y partiendo de los distintos sucesos se calculará la probabilidad de que se obtenga un envase defectuoso.
P(D)=[P(A) x P(D/A)]+[P(B) x P(B/A)]+[P(C) x P(C/A)]=
[0,4 x 0,02]+[0,3 x 0,03]+[0,3 x 0,05]=0,032
Es decir que la probabilidad de que un envase fabricado por la empresa en España sea defectuoso es de 3,2% expresándola en porcentaje.
Ahora si se adquire un envase y el mismo tiene defectos ¿Cuál es la probabilidad de que haya sido fabricado por la máquina A, la B o la C?

Aplicaremos el Teorema de Bayes ya que tenemos una información previa de que el envase es defectuoso, ahora queremos saber cuál es la probabilidad de que se haya producido por una de las maquinas de la fábrica:
P(A/D)= [P(A) x P(D/A)]/P(D)= [0,40 x 0,02]/0,032=0,25
P(B/D)= [P(B) x P(D/B]/P (D)= [0,30 x 0,03]/0,032= 0,28
P(C/D)=[P(C) x P(D/C)/P (D)= [0,30 x 0,05]/0,032=0,47
Con este se comprueba que sabiendo que un envase es defectuoso, la probabilidad de que haya sido producido por la máquina A es de 25%, por la máquina B es de 28% y por la máquina C es de 47%.
Esperamos que con este sencillo ejemplo hayas comprendido de mejor manera la forma en la que puedes aplicar el Teorema de Bayes.
